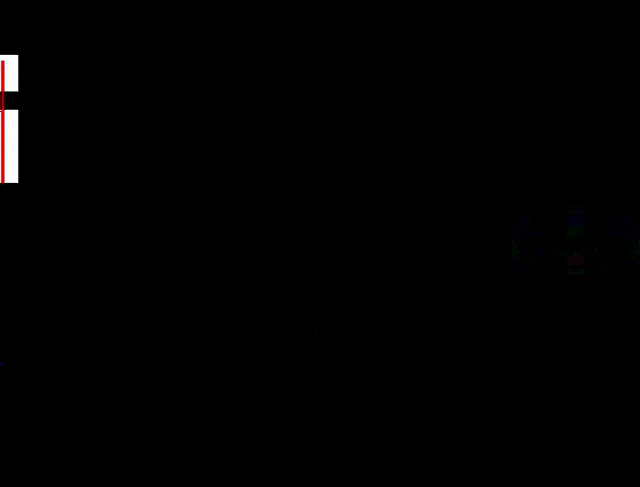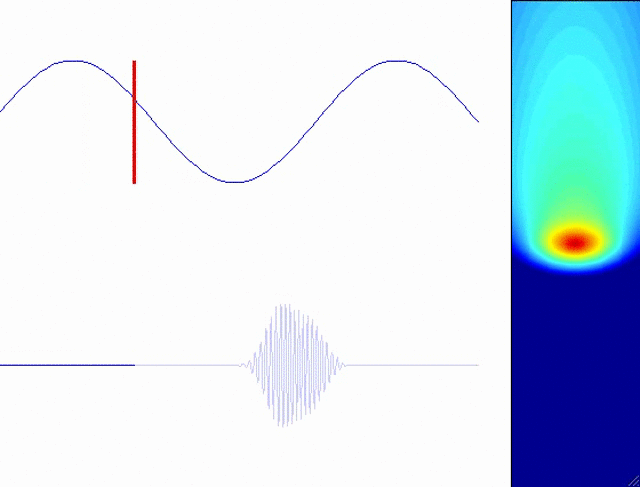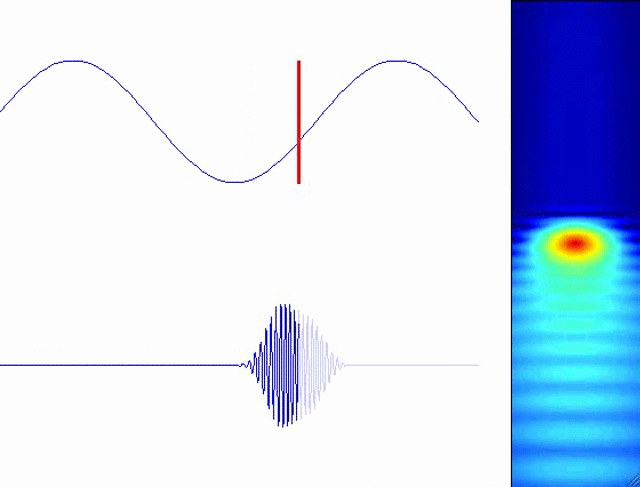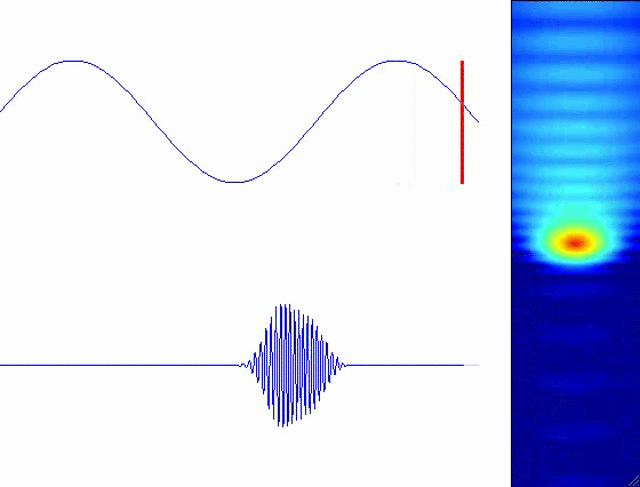Since the 1980s, laser amplifiers have been able to produce electric fields of comparable strength to the Coulomb force which binds an atom with its outer electrons. Such fields remove an electron from the atom or molecule. At this point, the electron behaves like a free charged particle, moving under the influence of the laser field. In particular it may be accelerated to high velocities (up to several hundred electron volts), whilst still remaining in the vicinity of the atom. When the field changes direction, as happens twice every optical cycle (approximately 1015 times per second), the electron is driven back towards the atom, and an inelastic collision occurs. The liberated energy is converted into a photon, with wavelength in the extreme ultraviolet or soft x-ray regions.

In reality, the electron’s wavelike nature is important in high-order harmonic generation. Furthermore, ionization occurs at every peak of the laser field, leading to a complex electronic wavefunction which can be simulated using the time-dependent Schrödinger equation (TDSE). I have developed codes for solving the TDSE. This figure shows a typical solution in one spatial dimension, represented by the modulus-squared of the wavefunction:

The following animation shows the HHG process for a single half-cycle of the laser field. The field is vertically polarized. The lower blue curve shows the emitted XUV radiation burst.