Quantitative analytic theory of the single-atom response
The radiation emitted in high-order harmonic generation (HHG) can be calculated quite accurately using the time-dependent Schrödinger equation. (As ever, several approximations are necessary, the foremost being assumption of a single electron participating in the process, but this is sufficient for predicting most features of atomic HHG.) However, there is great advantage in analytic or semi-analytic approximate formulae based on approximate solutions to the TDSE. Most commonly, one ignores the effect of the ionic potential on the electron after ionization, instead treating the electron like a free charged particle. This is the ubiquitous strong-field approximation. The SFA treatment of HHG naturally reproduces the classical three-step model of ionization, acceleration of the free electron by the laser field, and recombination at the ionic core. Furthermore, it dramatically reduces the computational complexity of evaluating the HHG response.
However, in general it has proven difficult to obtain quantitative agreement between the results of TDSE calculations and the SFA, particularly in the absolute yield. This is particularly true for predictions of the scaling of the HHG single-atom response with the wavelength of the driving laser. This is a question of great importance increasing the drive wavelength carries benefits for phase-matching the generation of harmonics in the soft x-ray region.
Using the SFA and stationary-phase integrals, I derived an expression for the single-atom response in high-order harmonic generation which evaluates directly in the frequency domain. It may therefore be compared directly against spectra calculated using the TDSE, whilst simultaneously exposing all the relevant physical effects.
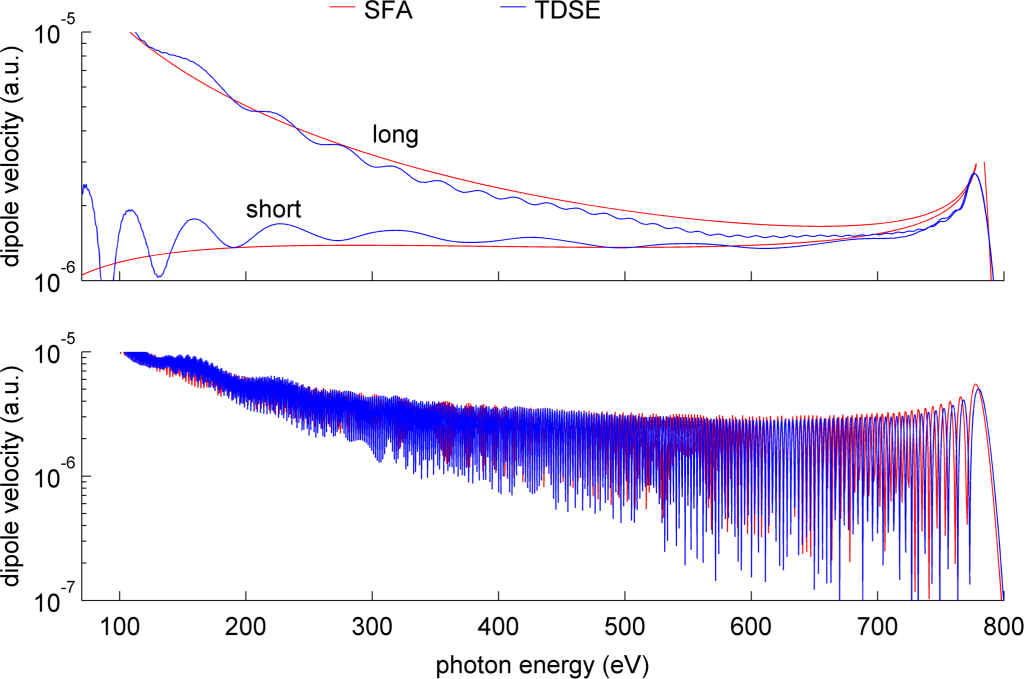
The following figure compares the spectra of the single-atom response predicted by the time-dependent Schrödinger equation (blue) and our formulation of the SFA. The laser field is a single-cycle mid-infrared pulse. In the upper plot, the contributions from the short and long trajectories are separated below the cutoff, whilst the lower plot shows the combined response, and therefore exhibits quantum-path interference. No scaling factors have been applied: the SFA accurately predicts the absolute amplitude of the response.
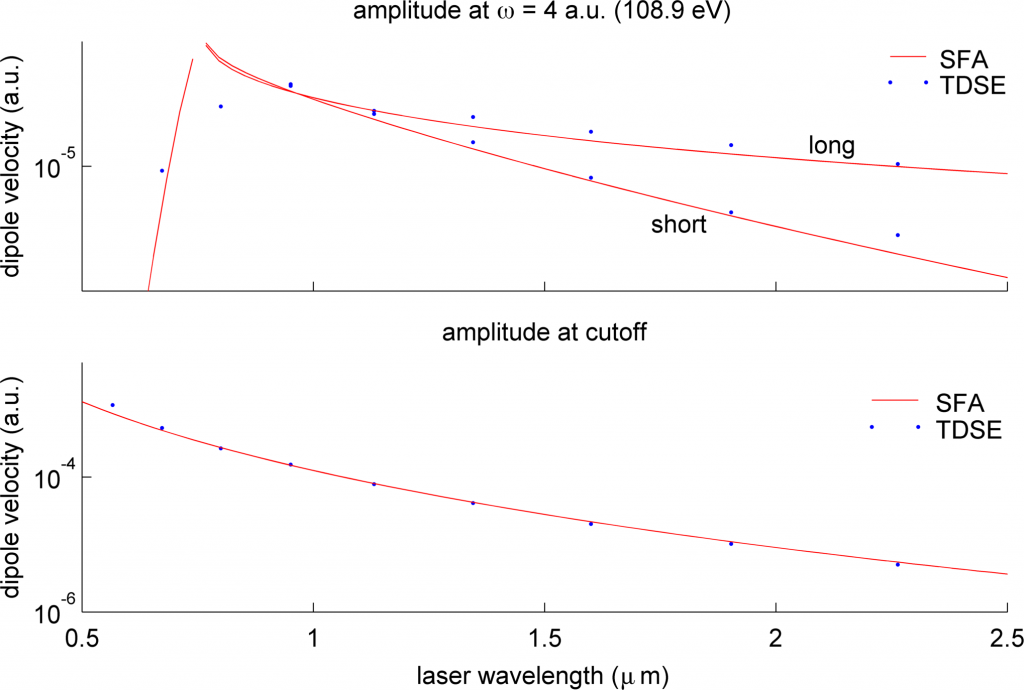
Our formulation of the SFA also correctly describes the scaling of the single-atom response with drive wavelength. The following figure shows the the amplitude of the single-atom response versus drive wavelength predicted by the TDSE and the SFA. The top plot shows single-atom response at a fixed harmonic frequency. As the drive wavelength is increased, this harmonic goes from being beyond the cutoff to below it, and short and long trajectories can contribute separately. The SFA reproduces the TDSE results across the wavelength range 566-2260 nm, which was limited by the computational demands of the TDSE. The second plot shows the amplitude at the cutoff harmonic frequency, which increases as the drive wavelength is increased. Again, there is excellent agreement.